BFOIT - Introduction to Computer Programming

Practice Answers: Expressions and Plumbing Diagrams

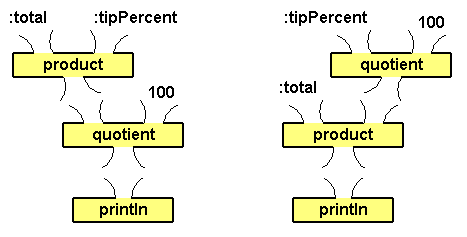
  1. Draw a plumbing diagram for a tip calculator which takes two numbers as inputs: the bill's total cost and the percentage of the tip.  The output of the expression (the amount of the tip) should be input to a println command box.
    Then write the procedure tipCalc which prints the tip amount... 
    to tipCalc :total :tipPercent
  println quotient (product :total :tipPercent) 100
  end
    Here are some sample computations and some inputs without the tip percent left for you to check your program with.
      Bill Total      Tip %       Tip $   
    $10
    15
    1.50
    $15
    20
    3.00
    $32
    16
    5.12
    $22
    18
    3.96
    $47
    17
    7.99
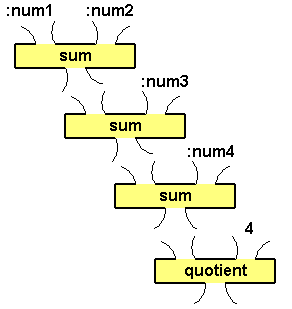
  2. The average of a bunch of numbers is the sum of the numbers divided by the number of numbers.

    Draw a plumbing diagram for the expression which averages four numbers.
    And like the similar plumbing diagram solutions above, you can switch around the inputs to the sum boxes.

    Write procedures to print the average of the numbers: 
    
(a)  66, 10, 47  (Average: 41)
(b)  22, 87, 15, 41  (Average: 42)
(c)  83, 31, 72, 19, 6  (Average: 43) 
    to avg3num :num1 :num2 :num3
  println quotient (sum (sum :num1 :num2) :num3) 3
  end

to avg4num :num1 :num2 :num3 :num4
  println quotient (sum (sum (sum :num1 :num2) :num3) :num4) 4
  end

to avg5num :num1 :num2 :num3 :num4 :num5
  println quotient (sum (sum (sum (sum :num1 :num2) :num3) :num4) :num5) 5
  end
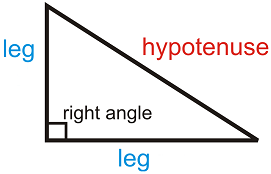
  3. Given Pythagoras' Theorem (the length of the hypotenuse of a right triangle is equal to the square root of the sum of the squares of each of its legs' lengths),
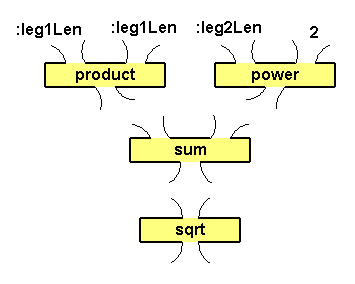
    Draw a plumbing diagram for this expression.
    Other correct plumbing diagrams may have two product boxes at the top, or two power boxes at the top, or the product and power boxes may be swapped with appropriate input changes.

    Then write a procedure which prints the length of the hypotenuse of a right triangle, given the lengths of its legs. 
    to hypotenuseLength :leg1Len :leg2Len
  println sqrt sum (product :leg1Len :leg1Len) (power :leg2Len 2)
  end

  4. Write procedures which display the surface area and the volume of a sphere, given its radius.  Here are the formulas you need. 
    
to sphereSurfaceArea :radius
  println product 4 (product 3.14159 (product :radius :radius))
  end

or

to sphereSurfaceArea :radius
  println product 4 (product 3.14159 (power :radius 2))
  end

and

to sphereVolume :radius
  println product (quotient 4 3) (product 3.14159 (product :radius (product :radius :radius)))  
  end

or

to sphereVolume :radius
  println product (quotient 4 3) (product 3.14159 (power :radius 3))
  end
    Fill in the empty cells with the values your procedures print rounded to thousandths.
    Unit
      Amount  
       Surface Area   
    (Unit2)
       Volume   
    (Unit3)
    1
    12.566
     4.189
    2
    50.265
    33.510
    3
    113.097
    113.097
    4
    201.062
    268.083
    Note: There are calculators on the net that compute the surface area and volume of a sphere.  Here is one I played with.  One thing to be aware of is rounding.  In order for me to get the Logo procedure output to match the calculator I had to use 3.14159265359 for pi (instead of just 3.14159).